文 | 巴曙松 蒋峰

一、引言及文献综述

2014年，“11超日债”利息无法按期全额支付，成为国内首例实质性违约的公募债券，中国债券市场“刚性兑付”就此终结。此后，我国债券市场信用违约事件频发，债券市场的违约风险开始集中释放。据Wind数据库统计，2016年、2017年违约债券数量分别为78只、49只，涉及债券余额分别为393.24亿元和392.90亿元。2018年受金融去杠杆、宏观经济增速下行、债券集中兑付等多方面影响，累计违约债券只数已达120只，违约余额高达1176.51亿元，信用风险大幅扩大。未来金融监管仍然以金融去杠杆、脱虚向实、严监管为主线，部分弱资质发债主体的融资仍将受到较大负面冲击，债券违约将常态化。如何看待近期债券市场违约事件增多？增多的原因有哪些？怎样防控债市信用风险？这一系列问题值得深入探索。

 

信用风险计量在信用风险管理领域处于核心地位，但目前信用风险的精准计量仍然存在较大难度。具有代表性的早期信用风险计量方法为专家法，通过专家对贷款人或债务人的信用状况进行定性的判定，现阶段专家法虽然在各行各业存在，但是由于其属于定性研究，相关文献较少。目前广泛采用的信用风险评估方法有：（1）基于信用转移分析的Credit Metrics模型，该方法由J. P. 摩根银行提出，广泛应用于商业银行贷款风险的评估，其核心在于企业信用等级的评估，同时将违约率、企业违约的相关性、违约损失率、信用转移矩阵等纳入模型，综合考虑信用风险度量问题；（2）麦肯锡公司开发出的宏观模拟模型——CPV模型，其通过建立一个多元经济计量模型来模拟出宏观经济运行状态，然后将宏观经济因素与信用评级转移概率之间的关系模型化，很大程度上克服了CreditMetrics模型关于不同时期评级转移矩阵固定不变的缺点；（3）CSFP（Credit Suisse Financial Products）提出的Credit Risk+模型，其思想源于保险精算学，该模型假设在不同时间段内违约人之间相互独立，与公司的资产结构无关，通过特定的概率生成函数，刻画贷款的损失分布，并将贷款损失分为若干个频段，计算在一定置信水平下每个频段的贷款损失，再进行加总计算总损失；（4）Moody公司的KMV模型，其基于布莱克—舒尔斯期权定价公式和Merton的风险债务定价理论计算贷款企业违约风险，主要计量上市公司和上市银行的违约概率、违约距离和违约损失。在上述模型中，KMV模型的主要数据来自于股票市场和财务报表，对公司信用方面的数据要求较少。同时在《巴塞尔资本协议Ⅲ》下KMV模型也受到巴塞尔委员会认可，并被列为商业银行内部评级法中有效的信用风险模型之一。我国的企业债券市场尚处于初级阶段,公司信用方面的数据比较匮乏，而股票市场和公司财务领域已积累了大量数据，同时随着我国股票市场股权分置改革基本完成，该模型的思路和处理方法在我国债券评估市场有广阔的应用前景。

 

目前国内外学者对于KMV模型的研究主要可分为模型的适用性、模型的应用与改进两个方面。张玲等（2004）通过对30家ST公司和30家非ST公司的实证研究，认为KMV模型适用于上市公司信用风险评估[1]；Duffie和Wang（2007）通过对国外公司历史数据的实证研究，认为KMV模型对企业的违约概率有很强的预测效果，同时构建了违约概率的期限结构[2]。蔡玉兰（2015）对KMV模型有效性来源进行了剖析，从理论上分析了违约距离对企业财务困境预测能力的来源[3]；Sreedhar和Tyler（2004）运用KMV模型对信用违约互换（CDS）中的信用价差进行解释，并论证了KMV模型对信用事件的预测能力[4]。张乃琦（2012）、刘澄和王大鹏（2011）、顾巧明和邱毅（2014）均采用KMV模型对地方政府债券违约风险进行了估计[5~7]；蒋彧和高瑜（2015）结合我国市场的变化对波动率、违约点等参数进行了修正[8]；刘珍珍等（2015）设计了5个不同指标代替资产价值增长率，实证表明单位平均资产的营业总收入增长率代替资产价值增长率时，模型识别能力最强[9]。

 

尽管国内外关于KMV模型的研究众多，但是仍然存在几点问题。一是模型输出的违约距离对违约概率的映射问题难以解决。国外成熟市场有大量的违约历史数据来构建违约数据库，但是我国违约数据并不够充分，国内有部分研究采用正态分布来映射，但是不少研究结果表明，这一方式会产生严重的失真问题。二是模型参数的修正问题，尤其是违约点设置问题不同，学者的实证结果略有不同，并且大多数实证的样本数据量较小，缺乏说服力。三是以往研究往往人为选取部分公司，或者选取单一行业样本，鲜有以整个市场为对象来研究当今国内经济市场各行业的行业风险水平。因此，本文在前人研究的基础上，通过违约距离这一指标测度信用风险大小，从而避免了以往文献中违约距离到违约概率映射方法上的争议，通过选取A股全部上市公司作为研究对象，将ST股近似地视为违约组，研究我国上市公司信用风险水平，设置违约预警线来评判上市公司信用风险水平大小，同时将市场各个行业的风险分别进行测度，分析当前经济环境下信用风险的行业异质性。

 

二、研究设计

 

（一）模型及其原理

 

1. KMV模型

 

在KMV模型中其假设当公司的股权价值（公司资产价值与债务价值之间的差额）为负，公司会存在违约的可能性，投资者也将面对公司的违约风险。传统的KMV模型主要分为三个步骤：第一步，通过公司的股权价值、股权价值波动率以及负债的账面价值估计公司的资产价值及其波动率；第二步，根据公司长短期负债计算出公司的违约点与违约距离；第三步，根据违约距离与违约概率的映射关系，求出违约概率。

 

 

根据违约距离的定义，可以知道其本身就能作为衡量违约风险的一个指标，违约距离越大，说明该公司到期偿还债务的可能性越高，越不可能发生违约，信用风险越低，反之，信用风险越高。通过违约距离求得违约概率EDF一般有两种方法，第一种方法假设公司资产价值的概率分布是已知的，根据中心极限定理，违约距离DD服从正态分布或者对数正态分布的前提下，可以直接计算出理论的期望违约概率。其公式为：

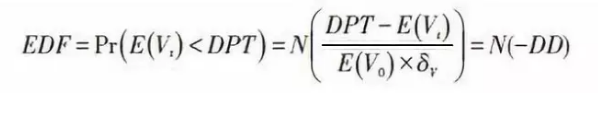
第二种方法则是通过大量的违约公司样本历史数据库，采用光滑曲线拟合的方式来表示违约距离与期望违约距离之间的函数关系，穆迪公司通过测试发现，违约距离与违约概率之间存在着稳定的函数关系。由于我国当前还没有公开的违约数据库可以使用，本文仅以违约距离DD作为上市公司信用评价指标。

 

2. 修正的KMV模型

 

作为全球最大的新兴市场之一，我国市场相较于其他发达国家成熟市场而言有其特殊性，这使得在运用传统的KMV模型测定违约风险过程中存在不便之处，主要包括违约数据不足、非流通股难以估值两方面的问题。同时传统的KMV模型自诞生以来，不少学者对其进行了改进，本文综合了以往研究中对传统KMV

 

模型的修正，并筛选出有效性较高的修正，应用于我国市场。

 

债券违约的界定问题。本文参照以往学者的做法将ST类公司视为违约样本[1][10~11]，这一处理主要是基于以下考虑。第一，我国资本市场的退出机制并不完善，而且以往即使公司处于违约的边缘，也能通过地方政府托底或者债务重组来避免违约，这为我们的研究带来极大的干扰。第二，在公司债务市场上，截至2018年8月仅有11家公司为上市公司，违约历史数据严重不足。第三，以往文献鲜有对于某一只特定债券违约风险的研究，公司作为发债主体当其发生财务状况恶化、信用恶化时，可能导致发行的债券出现批量恶化，以2018年永泰能源为例，其由于经营问题导致发行的8支债券违约，从企业债务状况不佳来反映违约风险具有一定的合理性。基于此，同时根据《股票上市规则》对被风险警示类公司财务状况的种种详细描述，可以看出ST类公司是极有可能违约的，所以，本文将出现财务状况恶化的ST股作为违约样本组，认为该类公司发生债券违约。由于我国A股市场的ST股数量较为可观，经过这一处理，本文构建了A股上市公司的公司债违约数据库，通过这一数据库结合列联表方法，设置了适用于我国市场的违约预警线，用于后续行业整体风险的测度。

 

非流通股的处理问题。我国上市公司股票分为流通股与非流通股两部分，流通股的价值与非流通股的价值无法对等，非流通股问题将导致无效的公司治理，上市公司与股东间的利益冲突无法均衡将导致公司更高的违约风险。之前的学者使用不同的转化方法来估算上市公司非流通股的价值，非流通股价值通常是以净资产与流通股价值为自变量的函数，而具体的函数关系至今也没有定论，不适当的修正都将导致偏颇的结论[12]。此外，2005—2013年以来，我国已经基本完成了股权分置改革，实际上已经消除了股权价值分割问题。非流通股解禁对A股市场确实有一定的影响，但并非影响A股市场资金面的根本因素。基于此，本文研究的数据均来自于2013年以后，同时用总市值直接表示上市公司股权价值。

 

（二）研究方法与思路

 

在传统的KMV模型中，模型的最终输出结果为期望违约概率EDF，其是由穆迪公司利用所有美国上市公司历史信息数据库将给定的违约距离DD进行映射而得，即给定违约距离DD下实际违约上市公司的比例，然而由于数据上的限制，我国计算准确的经验期望违约概率条件还不够充分。因此，本文直接采用违约距离DD，其含义为远离违约点DPT的资产价值百分比的资产价值标准差的个数，其是一个标准化的度量指标，而前人对我国上市公司的研究也指出不同的违约距离DD可以用来直接比较以反映不同信用主体的信用等级水平[2][13]。同时由于我国股票市场无法公开获得充足可用的上市公司实际违约数据（截至2018年8月发生实际违约的上市公司仅11家），因此我们遵循前人研究的经验，将那些特殊处理的上市公司（包括ST和*ST）视为违约上市公司[1][10~11]。本文的整体研究步骤如下：第一步，通过公司的股权价值、股权价值波动率以及负债的账面价值，借助KMV模型，估计公司的资产价值及其波动率；第二步，设置不同的违约点，计算出不同违约点下的违约距离DD值，选取最优的违约点，同时通过F检验比较违约组与对照组的违约距离有无显著差异，验证违约距离DD值是否是有效的信用风险度量指标；第三步，构建违约数据库，通过列联表方法设置违约预警线，测度各个行业的整体信用风险水平。

 

（三）样本与参数

 

1. 样本选择与描述

 

本文上市公司的数据来源于Wind数据库，选取的上市公司为除金融行业外的全部A股上市的公司，财务来源于2013—2017年各公司的年报，波动率数据来源于2013年1月1日—2017年12月31日共计5年的日收盘数据，将所有样本按照是否为风险警示股票分为两组，非ST股分为正常组，ST股为违约组，剔除一些数据缺失以及财务报表异常的公司，共计得到有效样本公司3243家，其中违约组78家，正常组3165家。

 

2. 变量定义与描述

 

在实证分析中，我们采用以下变量（如表1）进行分析：公司的股权价值E用上市公司股票的总市值来表示；公司债务的市场价值用公司的长期债务和短期债务加和表示。

 

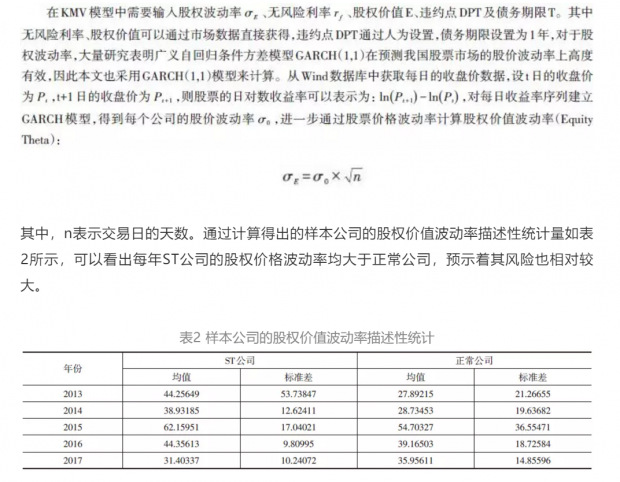
在无风险利率Rf的选择上，一般情况下无风险利率应当采用90天的国债收益率，但是由于我国的国债市场还不够完善，因此，本文采用加权的一年期定期存款利率来表示。时间设置为1年，即衡量1年期的信用风险水平。同时，在实证中本文对上市公司违约点DPT做如下假定：DPT=短期债务+α×长期债务，α 取0.1、0.2到1。

 

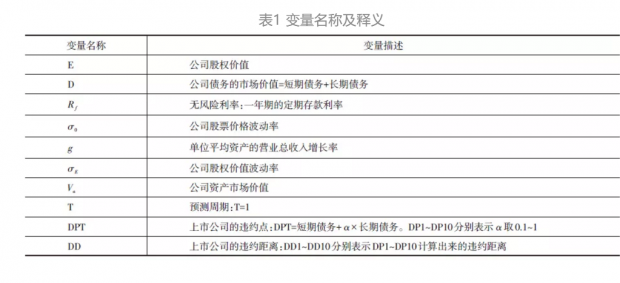
通过市场中获取的公司股权价值（Equity）、债务的市场价值（Debt）、无风险收益Rf、股权价值波动率（Equity Theta）建立KMV模型，通过Matlab软件计算出公司资产的市场价值（Va）和其波动率（Asset Theta）。最后再借助预先设置的违约点（DP1~DP10）计算出上市公司的违约距离（DD1~DD10），验证由违约距离到违约概率的映射是否适用于我国。

 

 

三、实证分析

 

（一）KMV模型的变量输入

 

 

 

（二）违约距离的计算

 

在KMV模型中，企业的信用风险主要取决于企业资产的市场价值、波动率以及负债价值。当企业资产未来市场价值低于企业所需清偿债务面值时，企业将违约。企业未来市场价值的期望值到违约点的距离就是违约距离DD。

 

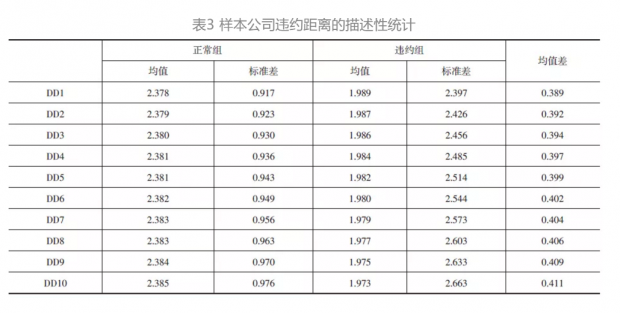
其中，x 取从0.1到1的10个数字，相应地求出DP1、DP2至DP10，经过上述模型可以得出相应的DD1、DD2到DD10。根据上述计算原理，借助MATLAB软件进行编程得到正常组和违约组各家公司的违约距离以及违约概率。违约距离的描述性统计量见表3。

（三）实证结果检验与分析

 

在KMV模型中，企业的信用风险主要取决于企业资产的市场价值、波动率以及负债价值。当企业资产未来市场价值低于企业所需清偿债务面值时，企业将违约。企业未来市场价值的期望值到违约点的距离就是违约距离DD。

 

1. 模型的检验

 

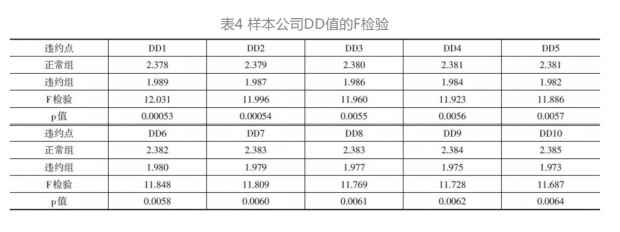
通过对表2中正常组和违约组DD值的均值差比较，可以初步看出违约点的选择并不会对违约距离产生大的影响，为了进一步说明这一情况采用F检验来验证。对正常组的违约距离和违约组的违约距离的分布进行F检验，原假设为正常组与违约组无显著差异。表4的F检验结果表明，F值均大于6.642，对应的在1%的置信区间内有效。而且不同的违约点对样本的F值也没有特别大的影响。根据对DD值的均值差比较和F检验结果，得出正常组的违约距离显著地高于违约组，即违约距离是衡量违约风险的有效指标，同时违约点的选取对违约距离无特别大的影响，参考以往的文献，在接下来的分析中将违约点设置为短期债务加上长期债务的一半，即DPT=Short Debt+0.5×Long Debt来进行分析。

 

 

2. 违约预警线的设置

 

基于上述过程中计算得到的违约距离，为了进一步量化我国上市公司的信用风险状况，本文采用了列联表的方式尝试着划定一条违约预警线，当上市公司的违约距离处于违约预警线下方时，可以认为具有较大的信用风险水平，列联表是观测数据按两个或更多属性分类时所列出的频数表，如表5。在本文中引用概率论中的两类错误Type Ι error、Type ΙΙ error。Type Ι error定义为模型中识别为正常组而实际为违约组；Type ΙΙ error定义为模型中识别为违约组而实际为正常组。

 

 

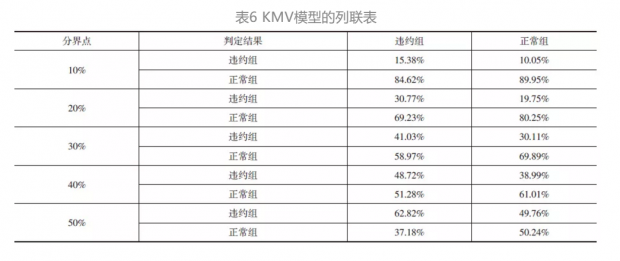
列联表可以直观地判定违约测度模型的好坏。以表5为例，表中的单元格分为四项：True Positive（TP）、True Negative（TN）、False Positive（FP）、False Negative（FN）。TP表示判定为违约组，实际上确实为违约组；TN表示判定为正常组，实际也为正常组。FN与FP定义为Type Ι error与Type ΙΙ error。最理想的状况为FN与FP都为0，这意味模型区分能力完美，但是实际上很难达到，Type Ι error的减小往往伴随着Type ΙΙ error的增大。由于本文的模型研究的是公司违约，FN出现的代价远大于FP出现的代价，因此模型首要追求较小的FN。结合本文的实证结果，得到KMV模型的列联表，如表6所示，当将分界点设置为全样本的10%时，发生Type Ι error的可能性极高，不断地提高分界点，当将分界点设置为50%时，发生Type Ι error与Type ΙΙ error的概率最小，因此根据全样本违约距离值的50%，参考这一结论将2.2设置为违约距离预警线。

 

 

3. 上市公司违约风险的行业特性分析

 

Wind数据库将我国上市公司分为18个行业，本文根据Wind的分类标准并将上市公司数量过小的行业剔除，将样本公司中正常组分为13个行业，分别计算各个行业违约距离的最值、均值与标准差。计算结果见表7。

 

 

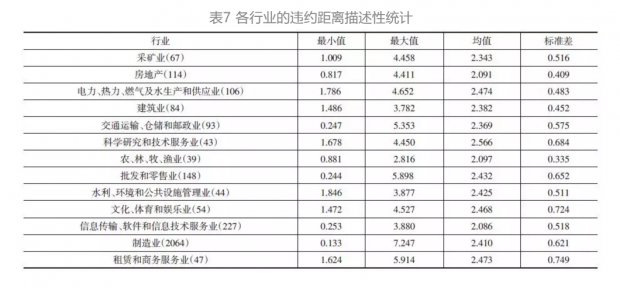
通过表7可以发现，从整体上来看我国各行业的平均违约距离没有显著低于违约预警线，各行业的违约距离标准差较小，这意味着每个行业违约风险整体离散程度较小，仅有部分企业信用风险较高；从各个行业违约距离的视角来看，共3个行业的违约距离均值处于预警线下方，分别为房地产业，信息传输、软件和信息技术服务业以及农、林、牧、渔业，这说明当前市场3个行业面临较大的违约风险。

 

四、结论及建议

 

为了研究上市公司信用债的违约风险大小，本文采用了调整后的KMV模型对A股市场全部上市公司的信用风险进行了量化，主要得出以下几点结论：第一，KMV模型计算出的违约距离能较好地反映整个市场的风险大小，公司的违约距离越大代表违约风险越小，以往关于KMV模型的研究中，由于违约样本不足等问题，往往都是基于几十家甚至几家公司进行的，缺乏对整个行业以及整个市场的大样本研究，本文将ST股近似地看成违约样本，将信用状况较差的公司与其他公司进行对比，论证了对于我国整个市场而言，KMV模型也是有效的；第二，通过计算出的违约距离，构建了我国公司债违约数据库，借助列联表进行分析，设置了上市公司的违约预警线为2.2，当计算出的违约距离小于2.2时，认为该公司存在较高的信用风险，投资者需要特别注意该公司信用债的违约风险，反之信用风险还是可控的；第三，结合实证结果对我国各个行业的信用风险进行了分析，从整体上而言，我国上市公司的信用风险可控，债券违约在未来将“常态化”，有序的债券违约将有益于市场的健康发展。

 

针对实证结果，在“违约潮”背景下应当关注信用风险的行业异质性，实行差异化管控。笔者认为，从行业角度来看，我国的房地产业，信息传输、软件和信息技术服务业以及农、林、牧、渔业存在较高的信用风险，相关部门应当重点关注，防范发生系统性风险。对于房地产行业而言，由于近年来我国房价处于历史高位，前期地产开发商在巨大的经济利益面前不断地开发新楼盘，这使得各地产公司四处融资，整个地产行业的负债率极高，同时受现阶段政府各项限购政策管制，房地产市场低迷，行业资金流动性较低，从而使得房地产企业的负债端与收入端全面承压，整体违约风险较高，因此需要重点防范房地产行业出现“爆雷”。对于信息传输、软件和信息技术服务业，由于云计算、AI等基础技术正持续影响并推动整个信息技术产业发生结构性变革，因此政府应当加大产业扶持力度，将自主可控导向的产业政策上升到国家高度，政策端与资金端共同发力，扶持优质信息技术服务企业发展，为经济发展注入新动能。对于以农、林、牧、渔业等为代表的第一产业而言，一方面该类行业的企业经营业绩具有一定的周期性，且受自然因素影响较大，整体缺乏稳定性，抗风险能力不强，而另一方面，其对我国经济的发展起着重要的支撑作用，是经济发展的命脉所在。结合这两方面的特性，国家政府应当充分发挥宏观调控作用，通过财政扶持、政策优惠等手段支持该类企业发展，防范该行业发生大规模信用风险。

 

参考文献

 

[1]张玲，杨贞柿，陈收.KMV模型在上市公司信用风险评价中的应用研究[J].系统工程，2004，(11):84-89.

 

[2]DuffieD, Saita L, Wang K. Multi-period Corporate Default Prediction with StochasticCovariates[J]. Journal of Financial Economics, 2007, 83(3): 635-665.

 

[3]蔡玉兰.KMV-Merton模型预测企业财务困境的有效性来源剖析[J].财会月刊，2015，(21):73-76.

 

[4]Sreedhar.T.Bharath，Tyler.shumway. Forecasting Defaulting With KMV-Merton Model[R].Working Paper，University of Michigan，2004.

 

[5]张乃琦.基于KMV模型的市政债券融资风险问题研究[J].经济与管理，2012，(8):38-42.

 

[6]刘澄，王大鹏.基于KMV模型的市政债券信用风险管理问题研究[J].中国管理信化，2011，(17):67-69.

 

[7]顾巧明，邱毅.我国地方政府债券信用风险测度研究[J].财经论丛，2014，(7):25-30.

 

[8]蒋彧，高瑜.基于KMV模型的中国上市公司信用风险评估研究[J].中央财经大学学报，2015，(9):38-45.

 

[9]刘珍珍，朱卫东，李玲玲.KMV模型中资产价值增长率的修正研究[J].财会通讯，2015，(15):112-115.

 

[10]王莉.引入违约距离的修正KMV模型在财务危机预警中的应用[J].统计与决策，2017，（17）：88-91.

 

[11]赵吉红，谢守红.我国制造业上市公司信用风险度量:基于KMV模型[J].财会月刊，2011，（30）：57-59.

 

[12]杨丹，魏韫新，叶建明.股权分置对中国资本市场实证研究的影响及模型修正[J].经济研究，2008，（3）：73-86.

 

[13]曹裕，陈霞，刘小静.违约距离视角下的开发性金融信用风险评估[J].财经理论与实践，2017，（5）：14-19.

 

作者简介：

巴曙松，北京大学汇丰金融研究院执行院长、中国银行业协会首席经济学家、香港交易所集团首席中国经济学家

蒋峰，中南财经政法大学金融学院金融工程硕士研究生

 

文章原载于《湖北经济学院学报》2019年11月（第17卷第6期），原题为：“违约潮”背景下的信用风险测度研究。